‘We have to remember that what we observe is not nature in itself but
nature exposed to our method of questioning.’
‘Debemos recordar que lo que
observamos no es la naturaleza en sí misma, sino la naturaleza expuesta a
nuestro método de cuestionamiento.’
Werner Heisenberg.
¿Cuándo se considera una teoría demostrada? Pues,
nunca realmente. Las teorías están basadas en experiencias anteriores e
intentan describir observaciones experimentales. El éxito de una teoría se mide
no solo por su habilidad para describir los hechos sino sobre todo por las
predicciones que hace en medidas aún no realizadas. Estas predicciones pueden
verse rechazadas por las medidas, lo que significa que la teoría no funciona
bien. En el caso contrario, una vez una teoría ha pasado varias pruebas
importantes, se puede considerar “aceptada” o “establecida”, pero nunca se
puede considerar demostrada de verdad.
Así sucede también
con la mecánica cuántica, la teoría que describe las propiedades y el comportamiento
de los sistemas físicos, especialmente a nivel microscópico. Las predicciones
de la mecánica cuántica se han verificado experimentalmente con un grado de
precisión impresionante, convirtiéndola en una teoría ampliamente aceptada.
A continuación,
hablaremos del mundo de las partículas subatómicas. Vamos a ver unos ejemplos
de propiedades de partículas que surgen de su naturaleza cuántica. Hablaremos
sobre todo de partículas que se producen en colisionadores de hadrones, como
por ejemplo los protones, y de leptones, como por ejemplo los electrones.
Aquí cabe recordar
cómo se producen dichas partículas, siendo Einstein el que propuso la
equivalencia entre masa y energía con su famosa fórmula E=mc2. En
los colisionadores, partículas cargadas y relativamente ligeras y abundantes en
nuestro entorno, como por ejemplo los electrones o los protones, se aceleran en
un campo electromagnético. Estas partículas alcanzan velocidades relativistas y
con ello energías cinéticas enormes. Volviendo a la fórmula de Einstein, su
energía se convierte en masa en la colisión. Así se producen nuevas partículas,
incluso algunas con una masa superior a la de los electrones y protones.
La
sección eficaz de colisión de electrones y positrones.
Como primer ejemplo, veamos qué obtenemos en una
colisión entre electrones y positrones. Ya se lo adelanto: el azar. Más
concretamente, no se puede predecir con seguridad qué va a suceder en una
colisión determinada. Lo que sí podemos conocer, con una incertidumbre
experimental por supuesto, es la probabilidad con la que se producirán unas
partículas u otras. En la Figura 1 les muestro la sección eficaz de la colisión
entre los electrones y sus antipartículas, los positrones, en función de la
energía en el sistema centro de masa. La sección eficaz es una medida de la
probabilidad de que se produzca un proceso específico en la interacción entre
las dos partículas.
En este caso se trata
de la probabilidad de producir hadrones, es decir, partículas compuestas por
quarks, o el bosón Z. En una colisión de electrones y positrones es posible
producir cualquier par quark-antiquark siempre y cuando lo permita la energía
de la colisión, o sea, siempre y cuando las masas de los quarks no superen
dicha energía. Los quarks, por su parte, forman hadrones que se observan en el
laboratorio. No se puede predecir qué se va a producir en una cierta colisión.
Lo que se conoce muy bien, en el caso de electrones y positrones, es la probabilidad
de crear cada tipo de par quark-antiquark. Si registramos muchas colisiones,
podremos predecir en qué proporción se producirá cada tipo de partícula. Este
conocimiento es muy importante por varias razones, de algunas de las cuales
volveremos a hablar.
Este histograma tiene
dos características principales. Primero, hay picos en ciertas energías a los
que llamamos resonancias. Estas resonancias son hadrones compuestos por un
quark y su correspondiente antiquark. Por ejemplo, la resonancia J/ѱ contiene un quark y un antiquark encantado. Dado
que la masa del J/ѱ está justo por
encima del doble de la masa del quark encantado, se trata de la resonancia más
ligera que contiene quarks de este tipo.
La segunda
característica del histograma son los “escalones” que encontramos justo después
de las resonancias. En estas regiones se pueden crear dos hadrones, cada uno de
los cuales contiene un quark adicional a los que se pueden producir por debajo
de dicha energía y un quark más ligero. Por ejemplo, después de ѱ(2S) se consiguen dos hadrones con un (anti-)quark
encantado y un quark (anti-quark) arriba, abajo o extraño.
Este histograma
recoge el saber de décadas de investigación desde los años 70 y grandes
cantidades de datos de varios proyectos experimentales de todo el mundo,
incluyendo aceleradores como ADONE (Italia), BEPC (China), DORIS y PETRA
(Alemania), CESR, PEP y SPEAR (Estados Unidos), TRISTAN (Japón) y VEPP (Rusia),
por nombrar algunos. El comportamiento de las secciones eficaces en función de
la energía es una prueba en favor de la teoría establecida de la física de
partículas, el Modelo Estándar, y en particular de nuestro conocimiento sobre
la interacción débil. Por ilustrar esto con un ejemplo, a continuación, nos
centraremos en medidas asociadas al bosón Z, la última partícula que puede
apreciarse en este histograma.
El
número de neutrinos “ligeros”.
El Modelo Estándar describe tres de las cuatro
interacciones fundamentales conocidas entre las partículas elementales – la
interacción fuerte, la interacción débil y la interacción electromagnética. El
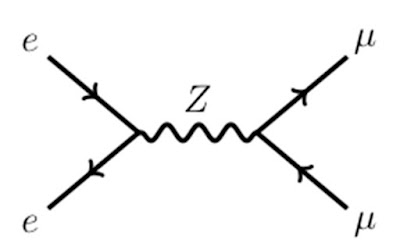
bosón Z es uno de los mediadores de la interacción débil, tal y como se muestra
en el proceso ilustrado en el diagrama de Feynman de la Figura 2. En este caso,
un electrón y un positrón se aniquilan para crear un bosón Z, el cual a su vez
se desintegra produciendo un muon y un anti-muon.
El bosón Z fue
descubierto de manera indirecta en 1973 en la cámara de burbujas Gargamelle en
el CERN, al observarse electrones que parecían moverse sin razón aparente. Esto
se interpretó como una interacción de los electrones con neutrinos invisibles,
en procesos como el mostrado en el diagrama de Feynman de la Figura 3.
En estos dos casos,
el bosón Z es una partícula virtual, lo que significa que existe durante un
tiempo tan corto que no es posible observarlo y medir sus propiedades de forma
directa. Pero como hemos visto en la primera figura, se han observado bosones Z
reales también en el laboratorio. Esto sucedió por primera vez en el año 1983,
de nuevo en el CERN, por los experimentos UA1 y UA2 situados en el Super Proton
Synchrotron. Por este descubrimiento y por el del bosón W, el cual se descubrió
en el mismo lugar y también es un mediador de la interacción débil, los físicos
Carlo Rubbia y Simon van der Meer recibieron el premio Nobel en el año 1984.
Las propiedades del
bosón Z se midieron con una precisión impresionante en el Large
Electron-Positron collider (LEP), un acelerador de electrones y positrones en
el CERN. El túnel de LEP, de una circunferencia de 27 kilómetros, se sigue
usando hoy en día por el acelerador de partículas más grande y de mayor energía
que existe, el Large Hadron Collider (LHC). LEP era el colisionador de leptones
más poderoso del mundo de su época y lo sigue siendo hasta el día de hoy. Operó
entre los años 1989 y 2000 y consiguió alcanzar una energía de 209 GeV. Uno de
los objetivos principales de los cuatro experimentos de LEP, llamados ALEPH,
DELPHI, OPAL y L3, era la medida de las propiedades del bosón Z, como por
ejemplo su masa y su anchura de desintegración.
La anchura de
desintegración, Γ, es una propiedad
relacionada con la vida media, τ, de las partículas inestables como el bosón Z. Estas dos propiedades son
inversamente proporcionales según el principio de incertidumbre energía-tiempo,
Γ
= ℏ · λ = ℏ / τ.
La anchura se
corresponde con la anchura a media altura del máximo de la curva de la sección eficaz
de desintegración en función de la energía. Tener una anchura en la masa
implica que una partícula no tiene una masa bien definida. Es decir, cada vez
que una partícula se desintegra, la energía que emite es algo distinta e
impredecible de manera exacta. Y aquí no se trata de una anchura que surge de
la resolución del detector sino de una propiedad cuántica de las resonancias.
En el caso del bosón
Z, la anchura nos da acceso indirecto a ciertas características muy
interesantes del Modelo Estándar. En particular, al número de neutrinos
ligeros, o sea, de los neutrinos más ligeros que la mitad de la masa del bosón
Z.
En el Modelo Estándar
hay tres generaciones de leptones cargados y, por lo tanto, uno esperaría que
haya tres tipos distintos de neutrinos. El bosón Z se puede desintegrar de
distintas maneras a pares de fermiones y anti-fermiones – quarks (todos menos
el quark cima, que es más masivo que el Z), leptones cargados (electrones,
muones, taus) y neutrinos. Si hay tres neutrinos más ligeros que el Z, uno
esperaría que uno de cada cinco bosones Z se desintegre a un par neutrino
anti-neutrino. Como los neutrinos no se pueden detectar directamente en los
detectores de los que disponemos en los aceleradores, su número se infiere de
manera indirecta. Esto equivale a medir la probabilidad de que el bosón Z se
desintegre en hadrones, Figura 4.
Si hubiera menos de
tres neutrinos, la probabilidad de desintegración del bosón Z a hadrones sería
más alta que la que predice el Modelo Estándar. En el caso de dos neutrinos,
los datos deberían coincidir con la línea roja superior. Y al revés, si hubiera
más de tres neutrinos, la tasa de desintegración del bosón Z a hadrones sería
más baja. En el caso de cuatro neutrinos, los datos deberían coincidir con la
línea roja inferior. Los datos confirman las predicciones del Modelo Estándar y
coinciden con la línea verde intermedia, la cual está de acuerdo con las
observaciones de una manera impresionante.
El
tiempo de desintegración.
Como ya hemos visto en la figura de las resonancias,
hay partículas que tienen anchuras grandes y viven muy poco tiempo y otras que
viven mucho más. Como en el caso de la masa, no se puede predecir cuánto tiempo
va a vivir una partícula, pero sí cuánto vivirá cada tipo de partícula en
promedio.
Hay varios aspectos
que definen el tiempo de desintegración promedio. Uno de ellos es el tipo de
interacción que da lugar a la desintegración. Por ejemplo, si comparamos la
interacción débil y la interacción fuerte, la segunda implica tiempos de
desintegración diez millones de veces más cortos. Otro factor es el espacio de
fases, es decir, las posibilidades que tiene una partícula para desintegrarse.
Si la diferencia entre la masa de la partícula y la suma de las masas de los
productos de desintegración es grande, el estado final dispone de muchas
posibilidades cinemáticas y los tiempos de desintegración se vuelven muy
cortos. Por ejemplo, la partícula elemental más masiva que conocemos, el quark
cima, tiene una masa tan grande que se desintegra antes de conseguir
hadronizar, esto es, antes de formar hadrones con otros quarks. Gracias a ello,
el quark cima nos permite estudiar un quark directamente y poner a prueba las
interacciones fuerte y débil.
La
física de sabor y las partículas que contienen un quark b.
El campo de la física que se dedica a estudiar los
quarks y los leptones se llama física de sabor por los seis tipos (sabores) de
quarks y leptones que conocemos. Es un campo muy activo hoy en día por las
diversas posibilidades que presenta para acceder a física más allá del Modelo
Estándar. A continuación, nos centraremos en hadrones que contienen un quark
fondo.
El quark fondo (b, de
beauty o bottom en inglés) se descubrió en 1977 por Fermilab y desde entonces
ha dado lugar a un campo de investigación continuo que nos ha aportado
descubrimientos esenciales. En 1987, el experimento ARGUS [5] descubrió que los
mesones neutros B0, los que están compuestos por un antiquark b y un
quark d, oscilan. Esto significa que los B0 se convierten en su
antipartícula, el anti-B0 (y al revés) conforme pasa el tiempo. Esta
propiedad de los mesones neutros surge de la interacción débil, tal y como
mostramos en el siguiente diagrama de Feynman para el caso del mesón B0s.
El mesón B0s
es un mesón neutro muy parecido al B0 con la única diferencia de que
el quark d está sustituido por un quark extraño. Los mesones B0s
y B0 oscilan de la misma manera. Sus quarks intercambian dos bosones
W, mediadores de la interacción débil, y el quark anti-b se convierte en un b,
mientras que el s se convierte en un anti-s, obteniendo de esta manera un anti-B0
a partir del B0 o un anti-B0s a
partir del B0s. Hay que notar de que en este caso se
producen también otras partículas virtuales, como por ejemplo un par
quark-antiquark cima, arriba o abajo. Por ello, midiendo estas oscilaciones se
puede acceder a las propiedades de las partículas virtuales, como por ejemplo
su masa.
Antes de entrar en
más detalle en las medidas de oscilaciones y su importancia, cabe notar que
fueron justamente las oscilaciones de B0 medidas por ARGUS las que
dieron los primeros indicios sobre la masa del quark más masivo, el quark cima.
Para sorpresa de todos, resultó que el quark cima es mucho más masivo de lo que
se esperaba. Para explicar las oscilaciones del B0, dicho quark
tenía que tener una masa de 50 GeV como mínimo. Tuvo que pasar casi una década
hasta que se descubrió el quark cima en Fermilab y, efectivamente, su masa
resultó ser de unos 173 GeV.
Desde este
descubrimiento y hasta hoy en día las medidas relacionadas con oscilaciones de
mesones B neutros siguen siendo muy relevantes. El descubrimiento de ARGUS
abrió la puerta a un nuevo tipo de experimentos, las llamadas fábricas de
mesones B. Dos experimentos de este tipo fueron construidos en los años 1990 en
colisionadores e+e-, Belle en Japón y BaBar en los
Estados Unidos. Los dos estaban basados en tecnologías similares y operaban a
la misma energía de colisión, 10.58 GeV, la masa de la resonancia Υ(4S).
La resonancia Υ(4S) decae en un mesón y un antimesón B neutros con
una probabilidad de alrededor de un 50%. Por razones cuánticas, este par está
en un estado coherente. Esto significa que en todo momento los dos mesones son
de sabores opuestos, B y anti-B y nunca un B y un B o un anti-B y un anti-B, hasta que uno de
los dos decae. A esta propiedad, el entrelazamiento cuántico, Einstein se
refería como “spooky action at a distance” (acción espeluznante a distancia).
Los dos mesones están en un estado común pero no intercambian información, no
interaccionan. Aun así “saben” en qué estado está el otro y conservan el estado
común hasta que la onda cuántica en la que existen los dos mesones se rompe.
Los mesones B tienen
una amplia gama de canales de desintegración. Entre ellos, la desintegración
del mesón B0 a dos mesones más ligeros, el J/ѱ y el K0S, tiene una gran
importancia en el campo de la física de partículas. En este canal de
desintegración, el Modelo Estándar predice una posible asimetría entre las
tasas de desintegración en función del tiempo de los mesones B0 y
los mesones anti-B0. Esta asimetría, llamada violación de la simetría CP
(de charge-parity en inglés, o simetría de carga paridad), representa un
papel importante en cosmología. La violación CP puede explicar, por
ejemplo, por qué existe más materia que antimateria en el universo.
Se puede determinar
la violación CP en el canal de desintegración B0→J/ѱ K0S midiendo por separado el
tiempo de desintegración de los dos tipos de mesones y por eso es importante
saber cuál de los dos se ha desintegrado. En esta medida, el entrelazamiento
cuántico de los mesones producidos en las fábricas de mesones B juega un papel
central. El estado final J/ѱ K0S es accesible tanto para un mesón B0
como para un anti-B0 y es aquí donde entra en juego el entrelazamiento
cuántico – en el momento de la desintegración se sabe que el otro mesón B0
(llamado B-tag, del inglés “tag” de etiquetaje) tiene el sabor contrario. A
partir de las desintegraciones del otro mesón B0 se puede determinar
su sabor y, de este modo, deducir el sabor del mesón B0 de interés,
que será el opuesto en este momento.
Los tiempos de
desintegración de los B0 y los anti-B0 medidos por Belle se muestran
en la figura. En azul puede verse el tiempo de desintegración de los B0
y en rojo el de los anti-B0. Lo que las fábricas de mesones B miden es el
tiempo Δt = t – ttag entre la desintegración del
mesón B0 de interés y el Btag. Como a veces el Btag
decae primero y a veces decae segundo, la diferencia del tiempo Δt puede ser positiva o negativa. Además, el tiempo
de desintegración es una función exponencial y como consecuencia de ello la
distribución de Δt consiste de dos funciones exponenciales de
espaldas y centradas en cero. La asimetría entre las dos distribuciones es muy
clara. Este resultado confirma que en el Modelo Estándar hay una diferencia
entre el comportamiento de los quarks y los antiquarks. Fue esta medida, junto
con la de BaBar en el mismo canal de desintegración, la que condujo al premio
Nobel de Física en 2008 para Makoto Kobayashi y Toshihilde Maskawa. Estos
físicos japoneses predijeron la asimetría CP, la cual exige la
existencia de por lo menos tres generaciones de quarks, ya en los años 1960,
cuando aún se conocían solamente dos generaciones.
Además de Belle y
BaBar hay también otros experimentos que se dedican a estudios de mesones B.
Además de los experimentos de LEP, esto incluye tres experimentos del LHC –
LHCb, ATLAS y CMS. Especialmente LHCb (de LHC Beauty) fue construido con el
objetivo de realizar medidas de hadrones conteniendo un quark b o c. Siendo un
experimento de colisiones de protones a una energía de múltiples TeV, el
principio de funcionamiento de LHCb es muy distinto al de las fábricas de
mesones B. Por un lado, los mesones B producidos en LHCb no están en pares
coherentes, lo que hace más difícil la identificación del sabor del mesón B.
Por otro lado, la sección eficaz de producción de mesones B es mucho más grande
y con esto LHCb tiene un conjunto de datos mucho mayor que las fábricas de
mesones B. Por último, los mesones B en LHCb se producen con una cantidad de
movimiento muy superior, lo que significa que decaen después de recorrer una
distancia significativa en el detector.
Esto es importante para medidas del tiempo de desintegración por razones
de la resolución del detector. El tiempo se mide a partir de la distancia entre
el punto de colisión de los protones y el punto de desintegración del mesón B.
Cuanto más larga es esta distancia, más precisa es su medida.
La resolución
temporal de LHCb es un orden de magnitud mejor que la de BaBar y Belle. Esto
abre la posibilidad a medidas como la de las oscilaciones de los mesones B0s,
que son un orden de magnitud más rápidas que las de los mesones B0.
No fue hasta 2006 que se observaron las oscilaciones en B0s
por el experimento CDF II de Fermilab, Estados Unidos [7], y las medidas
relacionadas con dichas oscilaciones siguen siendo muy relevantes en la
actualidad.
Recientemente, LHCb hizo una medida muy precisa de la oscilación del B0s midiendo el tiempo de desintegración del canal B0s→D-s π+ [8]. Las distribuciones del tiempo de desintegración de B0s y anti-B0s están mostradas en la Figura 7. Con el tiempo, algunos B0s se convierten en anti-B0s y viceversa, y por eso la tasa de desintegración sigue una sinusoide. En principio, el tiempo de desintegración es una función exponencial, pero en este caso una gran parte de los mesones B0s de los instantes iniciales no quedan registrados debido a las grandes cantidades de fondo y las limitaciones asociadas del experimento.
De la misma manera
que para las oscilaciones en B0, estudiar las oscilaciones del mesón
B0s provee información sobre la posible existencia de
nuevas partículas. Con respecto a esto, el último ejemplo del que me gustaría
hablar es la medida del canal de desintegración B0s→J/ѱ K K. Esta medida es uno de los objetivos
principales de LHCb y el Instituto de Física de Áltas Enerxías (IGFAE) y la
Universidad de Santiago de Compostela (USC) juegan un papel central en ella
[9]. Como hemos visto en el caso del mesón B0, sus oscilaciones nos
mostraron la existencia de una partícula que no se conocía hasta aquel momento,
el quark cima. Por la misma razón, para acceder a partículas que aún no
conocemos, medimos la violación CP en B0s→J/ѱ K K, la cual nos da acceso al contenido de la
oscilación, es decir, a las partículas que participan en la oscilación mostrada
en el diagrama de Feynman.
Hay varias medidas
que muestran que el Modelo Estándar es incompleto y varias teorías predicen la
existencia de partículas más allá de él. Estas partículas podrían ser muy
masivas y fuera del alcance del LHC. Pero podrían afectar a la oscilación de
los mesones B y alterarla con respecto a las predicciones del Modelo Estándar.
Dicha desviación sería una indicación indirecta de física más allá del Modelo
Estándar y por eso es muy interesante. En la última década se han medido
desviaciones en ciertos canales de desintegración de los mesones B [10] y la
medida de B0s→J/ѱ K K va a aportar información muy importante para resolverlas. En este
momento todas las medidas de violación CP en B0s→J/ѱ K K están de acuerdo con las predicciones del
Modelo Estándar, pero con más datos vamos a conseguir más precisión. Cuanto más
precisa sea la medida de B0s→J/ѱ K K, mejor vamos a entender la naturaleza de las
posibles partículas más allá del Modelo Estándar, incluyendo su masa y las
fuerzas con las que interaccionan.
Estas medidas y
muchas más van a aumentar en precisión en la próxima década, periodo en el que
tomarán datos los descendientes de Belle y LHCb, Belle II y LHCb Upgrade. Ambos
experimentos han mejorado sus detectores y van a aumentar la tasa con la que
toman datos. En unos años alcanzarán una precisión sin precedentes en los
canales de desintegración que he mencionado aquí, así como en muchos otros,
poniendo de este modo bajo un estricto examen al Modelo Estándar y,
posiblemente, haciendo descubrimientos revolucionarios.
En resumen, hemos
visto unos ejemplos de procesos del campo de la física de partículas muy bien
descritos por la mecánica cuántica. Esto es solo una parte muy pequeña de este
campo científico. En el siglo XX nuestro conocimiento del mundo de las
partículas subatómicas ha crecido de una manera enorme pero aún queda un camino
emocionante e inspirador por recorrer. En este sentido, me gustaría acabar con
una frase de Einstein con la que seguramente todos estaremos de acuerdo:
“Si Dios creó el mundo, su
principal preocupación ciertamente no fue facilitarnos su comprensión.”
Agradecimiento especial a: Avelino Vicente (IFIC) por la impagable ayuda en
la edición de este capítulo.
Referencias:
[1] P.A. Zyla et
al. (Particle Data Group), Prog. Theor. Exp. Phys. 2020, 083C01 (2020) and
2021 update
[2] Flip Tanedo, Quantum Diaries, https://www.quantumdiaries.org/2010/05/10/the-z-boson-and-resonances
[3] Wikipedia, https://en.wikipedia.org/wiki/Gargamelle
[4] The ALEPH Collaboration, The DELPHI Collaboration, The L3
Collaboration, The OPAL Collaboration, The SLD Collaboration, The LEP
Electroweak Working Group, The SLD Electroweak and Heavy Flavour Groups, “Precision
electroweak measurements on the Z resonance”, Physics Reports, Volume 427,
Issues 5–6, 2006, Pages 257-454
[5] Albrecht, H.; Andam, A.A.; Binder, U.; Böckmann, P.; Gläser, R.; et
al. (ARGUS Collaboration) (1987). "Observation of B0-anti-B0
mixing". Physics Letters B. Elsevier BV. 192 (1–2): 245–252.
[6] I. Adachi et al., “Precise measurement of the CP violation
parameter sin2ϕ1 in B0 → (cc)K0 decays”,
Phys. Rev. Lett. 108, 171802 (2012)
[7] A. Abulencia et al. (CDF collaboration), “Observation of B0s - anti-B0s
Oscillations”, Phys.Rev.Lett. 97: 242003, 2006
[8] LHCb collaboration, “Precise determination of the
B0s - anti-B0s oscillation frequency”, Nat. Phys. 18, 1-5 (2022)
[9] R. Aaij et al (LHCb collaboration), “Updated measurement of
time-dependent CP-violating observables in B0s→J/ψ K+K-
decays”
[10] R. Aaij et al (LHCb collaboration), “Test of lepton universality in
beauty-quark decays”, arXiv: 2103.11769 (enviado para su publicación a Nature
Physics)
Doctora en Física.







No hay comentarios:
Publicar un comentario