Uno de los principios
fundamentales de la Mecánica Cuántica consiste en la interpretación del estado
de un sistema físico como superposición de estados con propiedades definidas.
Si un cierto sistema puede encontrarse en diferentes estados en los que alguna
o varias de sus magnitudes físicas toman un valor distinto, hasta el momento en
que efectuemos una medida sobre él no podremos saber en cuál de entre todos los
estados posibles se encuentra y, por lo tanto, se encontraría potencialmente en
todos los estados simultáneamente. Expresado en términos probabilísticos,
existirá una cierta probabilidad de que el sistema se encuentre en una de las
posibles configuraciones y, en consecuencia, la medida de una de sus
propiedades tendría diferentes resultados posibles, cada uno con una
probabilidad asignada. De forma equivalente, podría decirse que, en el estado
inicial, esta magnitud física no estaría definida, pues una observación o
medida podría arrojar diferentes valores. Así, nos encontraríamos con estados
de un sistema que no tendrían bien establecidas ciertas magnitudes (estarían
formados por superposiciones cuánticas de estados con valores diferentes de las
mismas) pero sí podrían tener asignado un valor preciso de otro observable, lo
cual nos llevaría de nuevo al principio de incertidumbre de Heisenberg, tal y
como hemos descrito al inicio. Ciertas parejas de magnitudes podrían estar bien
definidas simultáneamente, mientras que no sería posible para otros pares de
observables, que solo podríamos medir con una cierta incertidumbre. Sin
embargo, la consecuencia más interesante de la superposición sería que, bajo
ciertas condiciones, las propiedades iniciales del sistema podrían cambiar
(oscilar entre los diferentes valores posibles) debido únicamente a la
existencia de los estados de superposición cuántica. El ejemplo más notable de
esta situación es la oscilación de partículas neutras, como los kaones neutros
o los neutrinos. En los dos casos se trata de resultados muy relevantes, que
han llevado a establecer los fundamentos del Modelo Estándar de Física de
Partículas, por un lado, y a la primera evidencia de física más allá del Modelo
Estándar, por el otro.
Oscilaciones
de kaones neutros.
Los kaones son partículas formadas por dos quarks2,
que son los constituyentes elementales de los que están compuestos también el
protón y el neutrón, y fueron descubiertos en 1947 estudiando los rayos
cósmicos [2]. Se trata de las primeras partículas conocidas que contienen un
nuevo quark, el quark s, al cual se asocia un nuevo número cuántico, la extrañeza.
En el caso de los kaones neutros, K0 y anti-K0, el
primero de ellos está formado por un quark d y un antiquark s,
mientras que el segundo se compone de un antiquark d y un quark s,
de forma que se trata de estados que tienen bien definido el número cuántico extrañeza:
s(K0) = +1 y s(anti-K0) = -1.
Los mesones K0 y
anti-K0 se producen en procesos mediados por la interacción fuerte,
que conserva extrañeza y, por tanto, si las partículas iniciales no contienen
quarks s, las partículas con extrañeza han de producirse por pares que
compensen la falta de extrañeza del estado inicial. Las masas de K0 y
anti-K0, calculadas por conservación de la energía en su proceso de
producción, son iguales y del orden de 1000 veces la masa del electrón. Sabemos
también que se trata de partículas inestables y que su desintegración, sin
embargo, ocurre por procesos de interacción débil, que no conserva extrañeza3.
Esto quiere decir que, a efectos de la interacción débil, K0 y
anti-K0 son partículas
idénticas, ya que la única propiedad que las distingue es irrelevante para este
tipo de procesos. Así, la interacción débil puede transformar un tipo de kaón
neutro en el otro, dando lugar a la oscilación
de los kaones neutros, representada
en la Fig. 1. En este diagrama, W es una de las partículas
mediadoras de la interacción débil y (u, c, t)4 son los
quarks que podrían producirse en el proceso debido a la mezcla entre quarks.
Esta mezcla, parametrizada a través de la matriz de Cabibbo-Kobayashi-Maskawa
[3], surge como consecuencia de la discordancia entre los estados de la
interacción débil y los estados con masa definida y es la responsable de todos
los procesos en los que se dan transmutaciones entre las familias de quarks,
como es el caso de las oscilaciones de kaones.
De acuerdo con la Fig. 1, si partimos por ejemplo de un estado inicial
formado exclusivamente por K0, al cabo de un rato algunos K0 se
habrán transformado en anti-K0,
de forma que nuestro sistema de kaones estará formado por una combinación de
K0 y anti-K0, en la que la proporción de cada uno de
ellos irá oscilando con el tiempo
Para acabar de complicar la situación, entraría en juego un tercer
observable: las propiedades de transformación bajo la simetría conjugación
de carga-paridad o simplemente CP. Esta simetría establece que las
leyes de la física deberían ser las mismas si una partícula se intercambia con
su antipartícula a la vez que se invierten sus coordenadas espaciales, y
resulta crucial para intentar explicar la asimetría materia-antimateria del
universo. En la desintegración de los kaones se observa que K0S
tiene una vida media más corta (su nombre procede de K-short) y decae a
dos piones, que es un estado con CP= +1, mientras que K0L tiene una vida
media más larga (K-long) y se desintegra generalmente a tres piones que
es un estado con CP = -1. Por tanto, si se deja evolucionar un haz de kaones
neutros, tras un lapso de tiempo cabría esperar que estuviera formado
exclusivamente por K0L,
de mayor vida media, y que el estado final consistiera siempre en tres piones.
Sin embargo, por cada 1000 desintegraciones a tres piones, se observaron
también varias desintegraciones a dos piones, indicando una violación de la
simetría CP en el proceso. Este resultado implica que las propiedades de
transformación bajo la simetría CP no están bien definidas en ninguna de las
parejas mencionadas anteriormente, (K0 - anti-K0) y
(K0L - K0S).
En cambio, existiría una tercera pareja con estas propiedades bien definidas
que, en lenguaje de la mecánica cuántica, diríamos son los autoestados del
operador CP o estados con CP definida: (K01 - K02). Esta
observación, realizada en el laboratorio de Brookhaven (Estados Unidos) en 1964
[4], supuso el descubrimiento de la violación de la simetría carga-paridad en
las interacciones electrodébiles, y por él recibieron el Premio Nobel de Física
de 1980 los físicos estadounidenses James Cronin y Val Fitch.
La observación de Cronin, Fitch y colaboradores demostró
la existencia de una violación indirecta de la simetría CP en las interacciones
electrodébiles, originada por la mezcla de kaones. Posteriormente,
la violación de la simetría CP ha sido observada de forma directa en la
desintegración de los kaones neutros en los experimentos KTeV (Fermilab) y NA48
(CERN). Más recientemente se ha observado procesos con violación de CP en
desintegraciones de otros sistemas de mesones neutros, como los mesones B0, los mesones D0 y los
mesones B0S. Sin
embargo, a diferencia de lo que ocurre con la violación de la simetría
paridad en las interacciones electrodébiles, que es del 100%, es decir, se
viola en todos los procesos, la magnitud de la violación de la simetría CP es
extremadamente pequeña. Por tanto, a pesar de que su existencia podría en
principio explicar el origen de la asimetría materia-antimateria del universo5,
el valor medido experimentalmente queda varios órdenes de magnitud por debajo
de la cantidad de violación de CP requerida para explicar el desequilibrio
entre la materia y la antimateria observado. Así, si creemos que se llegó hasta
el universo actual debido a una violación de la simetría CP, debemos ir a
buscar a otro sector, como el de los neutrinos. Esto nos lleva al segundo
escenario del que hablaremos en este artículo: las oscilaciones de sabor de los
neutrinos.
Oscilaciones
de sabor de los neutrinos.
Los neutrinos son unas de las partículas más
abundantes del universo, solo superadas por los fotones. Sin embargo, son
también las partículas que más desconocemos y las que han proporcionado la
primera evidencia de física más allá del Modelo Estándar. Pero vayamos poco a
poco.
Los neutrinos, como
su nombre indica, son partículas neutras, sin carga eléctrica, y se producen en
procesos mediados por la interacción débil, como la desintegración nuclear de
tipo beta o la fusión nuclear. Además, solo interaccionan con la materia a
través de este tipo de procesos (son insensibles a la fuerza electromagnética y
a la interacción nuclear fuerte), por lo que resulta realmente difícil
detectarlos. Esto explica que su descubrimiento se hiciera esperar más de 25
años desde que Wolfgang Pauli postulara su existencia para salvar la
conservación de energía en procesos de desintegración nuclear [5]. Hoy sabemos que existen tres tipos de
neutrinos con propiedades de interacción bien definidas: el neutrino
electrónico o ne,
que interacciona por procesos débiles de corriente cargada con el electrón, el
neutrino muónico nm, que lo hace con el
muon, y el neutrino tau nt que interacciona por
corrientes cargadas con el leptón tau. Por otro lado, según el Modelo Estándar,
los neutrinos son partículas sin masa, igual que los fotones, aunque, como
veremos, los neutrinos han venido acompañados de algunas sorpresas.
El neutrino
electrónico fue descubierto por Frederick Reines y Clyde Cowan en 1956 en la
planta nuclear de Savannah River (Georgia, Estados Unidos)6. En
concreto, este primer neutrino observado (indirectamente, pues es la única
forma de detectarlos) era un antineutrino electrónico. Poco tiempo después,
Raymond Davis Jr. conseguía observar neutrinos electrónicos producidos en el
Sol (conocidos como neutrinos solares) desde su experimento situado en las
profundidades de una mina de oro en Homestake (Dakota del Sur, Estados Unidos).
Este experimento fue concebido para probar la validez de los modelos estelares
según los cuales el Sol (y el resto de estrellas) brillan debido a los procesos
nucleares de fusión que tienen lugar en su interior, en los cuales se emite un
número ingente de neutrinos, del orden de 10.000 millones por segundo y por
centímetro cuadrado.
Sin embargo, las
primeras medidas del experimento Homestake, realizadas en 1968 arrojaron solo
un tercio del número esperado de neutrinos. De esta forma comenzó el conocido
como problema de los neutrinos solares. Esta discrepancia entre las
predicciones teóricas y las observaciones experimentales fue atribuida en
primer lugar al modelo solar, dada la complejidad del mismo. Sin embargo, este
modelo, desarrollado por el astrofísico John Bahcall, fue refinándose con el
tiempo y otras de sus predicciones fueron validadas de forma independiente
[6]. Del mismo modo, la posible existencia de errores experimentales fue
descartada cuando nuevos experimentos utilizando diferentes técnicas siguieron
observando un déficit en el número de los neutrinos solares medidos en la
Tierra. Así pues, tras décadas de esfuerzos teóricos y experimentales, parecía
que la única solución posible era que alguna cosa estuviera ocurriendo a los
neutrinos desde su producción en el Sol hasta su llegada a la Tierra. Diversas
soluciones fueron propuestas, aunque la definitiva llegó como respuesta a otra
anomalía, la observada en los neutrinos atmosféricos.
Los neutrinos
atmosféricos se producen tras la interacción de rayos cósmicos, en su mayoría
protones o núcleos ionizados de átomos ligeros, con núcleos de nitrógeno y
oxígeno de la atmósfera terrestre. Estos procesos desatan lluvias hadrónicas de
partículas que generan un gran número de partículas inestables como piones o
kaones que acaban desintegrándose a muones, y éstos a electrones y neutrinos,
en una proporción aproximada de dos neutrinos muónicos por cada neutrino
electrónico. Este flujo de partículas comenzó a estudiarse como ruido de fondo
en experimentos de búsqueda de desintegración del protón, pero la discrepancia
entre las predicciones teóricas y las observaciones pronto lo convirtieron en
un objeto central de estudio. Y es que el número de neutrinos muónicos
detectados (puntos en el panel derecho de la Fig. 5) era sensiblemente menor al
indicado por los cálculos teóricos (barras horizontales) y, además, dependía
del ángulo de llegada de los neutrinos al detector, de forma que el déficit era
más importante en el flujo de neutrinos que llegaba desde la vertical inferior
del detector, es decir, desde el otro lado de la Tierra (cos Q = -1), tras haber viajado mayores distancias. Los
resultados para los neutrinos electrónicos, en cambio, eran compatibles con las
predicciones teóricas (panel central en la Fig. 5).
Tal y como sucedió en
el caso de los neutrinos solares, diferentes mecanismos fueron propuestos para
explicar la desaparición de los neutrinos muónicos en el flujo atmosférico.
Finalmente, los resultados más precisos del experimento Super-Kamiokande, en
Japón, indicaron que la única solución compatible con las observaciones eran
las oscilaciones de sabor en el canal nm→nt. Esta transformación
explicaba por qué el número de neutrinos muónicos era menor del esperado sin
afectar a las medidas de neutrinos
electrónicos, explicando además el patrón de energías y distancias observado.
Las implicaciones de este resultado son enormes, ya que las oscilaciones de
sabor de los neutrinos pueden producirse únicamente si éstos tienen masa, en
contra de lo que predice el Modelo Estándar de física de partículas. En
consecuencia, las oscilaciones de neutrinos proporcionaron la primera prueba de
la existencia de nueva física, poniendo de manifiesto la necesidad de extender
el Modelo Estándar con la incorporación de nuevos mecanismos capaces de
explicar el origen de la masa de los neutrinos.
Tras la resolución de
la anomalía de los neutrinos atmosféricos en el detector japonés
Super-Kamiokande, otros dos experimentos realizaron observaciones que
consiguieron explicar también el problema de los neutrinos solares. Por un
lado, SNO, el Observatorio de Neutrinos de Sudbury (Ontario, Canadá) fue capaz
de medir de forma separada los neutrinos electrónicos (producidos en el Sol) y
del resto de sabores utilizando procesos débiles de corrientes cargadas
(sensibles solo a los ne) y de corrientes neutras (sensibles también a nm y nt), demostrando que no
había ningún déficit en el número de neutrinos solares que llegaban a la Tierra
[10]. El detector observaba todos los neutrinos esperados teóricamente según el
Modelo Estándar Solar (SSM), solo que, durante su camino hacia nosotros,
algunos de los ne (aproximadamente dos tercios) habían mutado a
neutrinos de sabor diferente, nm y nt (Fig.
6, panel izquierdo). Por tanto, el misterio estaba parcialmente resuelto, y
digo parcialmente porque se sabía que se habían transformado, pero no cómo lo
habían hecho, ya que diferentes mecanismos podían explicar satisfactoriamente
la mutación. Entonces llegó el resultado del experimento de reactor KamLAND,
también en Japón. Su objetivo consistía en buscar oscilaciones de antineutrinos
electrónicos, pues su existencia supondría la confirmación del mecanismo de
oscilación como solución al problema de los neutrinos solares. En 2002, KamLAND
observó un número de anti-ne menor del esperado y compatible con el mecanismo de
oscilaciones de sabor, y dos años después obtuvo la prueba irrefutable de las
oscilaciones: una variación del número de neutrinos con la energía y la
distancia recorrida que solo este mecanismo podía explicar (Fig, 6, panel
derecho). De esta forma quedó también confirmada la existencia de las
oscilaciones de sabor en el sector de los neutrinos solares.
Este resultado, junto
el descu-brimiento de las oscilaciones de neutrinos atmosféricos sirvió para
otorgar el Premio Nobel de Física de 2015 a Takaaki Kajita y Arthur McDonald,
máximos responsables de los experimentos Super-Kamiokande y SNO,
respectivamente. Posteriormente, el fenómeno de oscilaciones de neutrinos ha
sido observado en una gran variedad de experimentos, utilizando fuentes
naturales, como los neutrinos solares y atmosféricos, así como fuentes
artificiales, en experimentos de reactor y acelerador.
Pero, ¿cuál es el
mecanismo por el que se producen las oscilaciones de neutrinos? Como hemos
comentado anteriormente, la clave está en su masa, y en la existencia de
diferentes estados con ciertas propiedades definidas y otras no, como vimos
para los kaones. Si los neutrinos son partículas masivas, los estados de
neutrinos con masa definida, a los que nos referiremos como (n1, n2, n3)
serán, en general, diferentes a los estados con sabor definido, (
donde se ha usado notación cij = cosθij
y sij = sinθij para los 3
ángulos de rotación θ12, θ23 y θ13 que definen
la transformación unitaria. El cuarto parámetro, δ, es el
responsable de la violación de la simetría CP en el sector de los neutrinos y,
por tanto, de él depende que los neutrinos y sus antipartículas, los
antineutrinos, se comporten de forma diferente.
Los neutrinos se
producen en procesos de interacción débil y, por tanto, en la producción
tendremos estados con un sabor definido: electrónico, muónico o tau que, a su
vez, consistirán en una combinación de los estados con masa definida (n1, n2, n3),
según la matriz de mezcla de la Eq. (1). Puesto que sus masas no son
exactamente iguales, la evolución de cada ni (i=1,2,3) a medida que van propagándose por el
espacio es ligeramente diferente, lo cual resulta en una proporción de n1, n2 y n3 distinta a la inicial y, por tanto, un estado de
sabor definido diferente. De esta forma, se habría producido una oscilación
entre el neutrino inicial, con un sabor concreto nα, y
el final con un sabor diferente, nβ.
La clave de esta
oscilación se encuentra en que los neutrinos tengan masa y en que, además,
estas masas sean diferentes. De hecho, la probabilidad de oscilación de los
neutrinos dependerá, por un lado, de los ángulos de mezcla de la Eq. (1) y la
Fig. 8, y de las diferencias entre sus masas, por otro. En ciertos casos es
posible simplificar el cálculo de la probabilidad de oscilación considerando
solo dos familias de neutrinos, y el resultado sería el siguiente:
donde θ sería uno de los ángulos de la matriz de
mezcla, L la distancia viajada por el neutrino entre su producción y su
detección, E su energía, y Δm2 la diferencia de masas al cuadrado
entre dos de los estados con masa definida: (mi2-mj2).
Por tanto, vemos que las oscilaciones dependen de las diferencias de masas
entre los neutrinos, pero no de su escala de masa absoluta, así que no pueden
proporcionar información acerca de la misma. A día de hoy se ha conseguido
medir con muy buena precisión el valor absoluto de las dos diferencias de masas
entre los tres neutrinos, pero aún no hemos podido establecer el signo de una
de ellas, de forma que los estados de masa se pueden organizar de dos formas
posibles, tal y como indica la Fig. 9. La primera de ellas se conoce
como orden normal (NO, izquierda) y la segunda como orden inverso (IO,
derecha). Los colores indican la fracción de los estados de sabor (νe, νμ, ντ)
contenida en los estados de masa (ν1, ν2, ν3),
en función de los parámetros de oscilación.
Utilizando los
resultados de todos los experimentos de oscilaciones de neutrinos y a través de
los llamados análisis globales de oscilaciones, es posible combinar toda la
información disponible y explotar la complementariedad de los diferentes
conjuntos de datos para obtener medidas muy precisas de la mayoría de los
parámetros responsables de las oscilaciones de neutrinos. Esto nos ha permitido
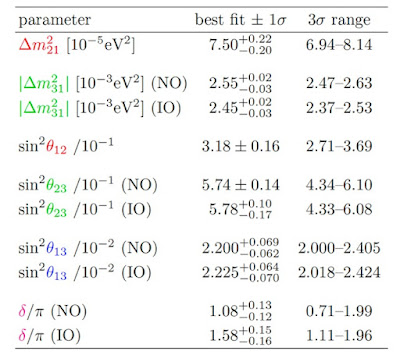
determinar los valores de los ángulos de mezcla θij y las
diferencias de masas Δm2ij con precisiones de entre el 1
y el 5%, ver Tabla 1. Las medidas de la fase de violación de CP, δ, todavía no
son tan precisas, pero se espera una mejora en el futuro cercano gracias a los
experimentos de acelerador actuales T2K y NOvA y, a más largo plazo, en los
futuros experimentos DUNE y Hyper-Kamiokande. Del mismo modo, nuevos resultados
de estos experimentos, así como de los telescopios de neutrinos IceCube y
KM3NeT permitirán establecer el orden correcto del espectro de masas de los
neutrinos, de entre los dos mostrados en la Fig. 9. De esta forma quedarán
resueltas las incógnitas pendientes relativas al mecanismo de oscilación de los
neutrinos, lo cual permitirá nuevos avances en las búsquedas de física más allá
del Modelo Estándar.
Y aquí acaba este
viaje que nos ha llevado desde los fundamentos de la mecánica cuántica hasta
dos grandes descubrimientos que han servido, en primer lugar, para establecer
los fundamentos del Modelo Estándar de física de partículas y, unas décadas
después, para ponerlo en tela de juicio e impulsar la búsqueda de nuevas
teorías capaces de acomodar las masas de los neutrinos. Queda pendiente también
la conexión de la violación de la simetría CP en el sector de los neutrinos con
la asimetría bariónica del universo. A través del estudio de las oscilaciones
de neutrinos y de antineutrinos en los experimentos actuales y de nueva
generación, en unos años seremos capaces de establecer con precisión la
magnitud de esta asimetría CP y aclarar si podría tratarse de un ingrediente capaz
de explicar la naturaleza de nuestro universo.
Notas:
1 Aunque, en muchos aspectos, la física cuántica es
tan determinista como la clásica.
2 Las partículas compuestas de dos quarks (en
realidad una pareja quark-antiquark) reciben el nombre de mesones.
3 No existe otra opción, ya que se trata de las
partículas extrañas más ligeras que existen y, por tanto, su desintegración no
puede conservar la extrañeza.
4 Nótese que la existencia del cuarto quark (charm
o c), así como de la tercera generación (quarks b y t) fue
propuesta antes de su descubrimiento a partir del estudio de las oscilaciones
de los kaones neutros.
5 Una pequeña diferencia en el comportamiento de la
materia y la antimateria en el universo primigenio podría explicar la pequeña
asimetría entre ambas que dio lugar al universo dominado por la materia en el
que vivimos. Esta diferencia podría ser explicada en términos de la violación
de la simetría CP.
6 F. Reines recibió el Premio Nobel de Física en 1995
por este descubrimiento.
Referencias:
[1] N. David Mermin, Physics Today 57, 5, 10 (2004).
[2] G. Rochester, C. Butler, Nature 160, 855–857
(1947).
[3]
P.A. Zyla et al. (Particle Data Group), Prog. Theor. Exp. Phys. 083C01 (2020).
[4] J.H. Christenson, J.W. Cronin, V.L. Fitch, R. Turlay, Phys. Rev. Lett. 13 138-140
(1964).
[5] https://www.symmetrymagazine.org/article/march-2007/neutrino-invention
[6] J. N. Bahcall, Nucl. Phys. Proc. Suppl.
118, 77-86 (2003), [arXiv:astro-ph/0209080v2].
[7] G. Orebi Gann, K. Zuber, D. Bemmerer, A. Serenelli, Ann. Rev. Nucl. Part. Sci.
71, 491-528 (2021).
[8] W. Haxton, R. Hamish Robertson, A. Serenelli, Ann. Rev. Astron. Astrophys.
51, 21-61 (2013).
[9] T. Kajita, Rep. Prog. Phys. 69,
1607 (2006).
[10] Q.R. Ahmad et al. (SNO Collaboration), Phys. Rev. Lett. 89, 011301
(2002).
[11] T. Araki et al. (KamLAND Collaboration), Phys. Rev. Lett. 94, 081801 (2005).
[12] P. De Salas, S.
Gariazzo, O. Mena, C.A. Ternes, M. Tórtola, Front. Astron. Space Sci. 5, 36 (2018).
[13] P. De Salas et
al., JHEP 02, 071 (2021). [https://globalfit.astroparticles.es/]
Doctora en Física.









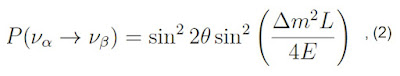

No hay comentarios:
Publicar un comentario